Sortings

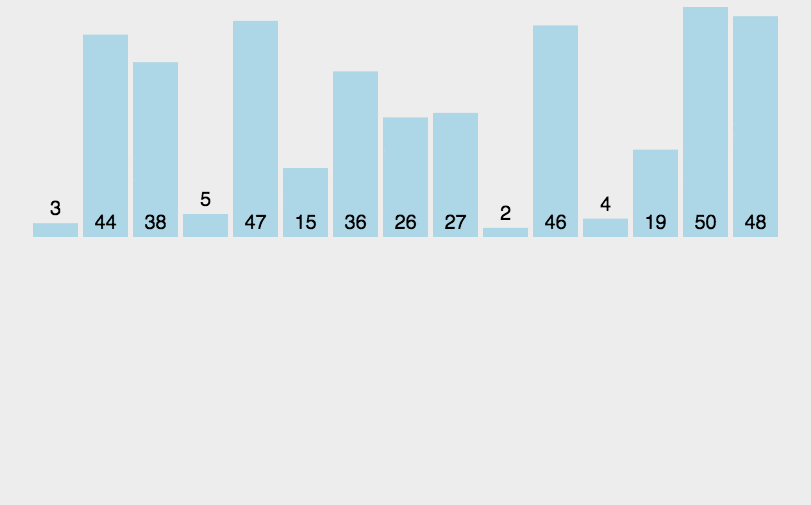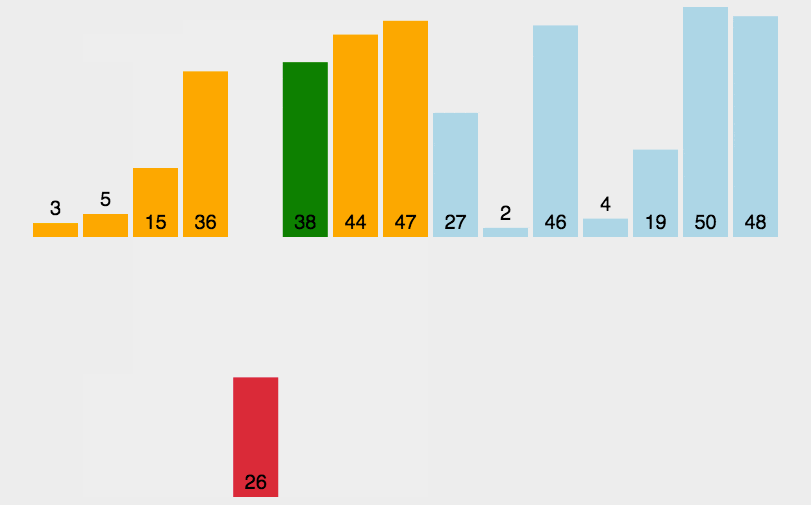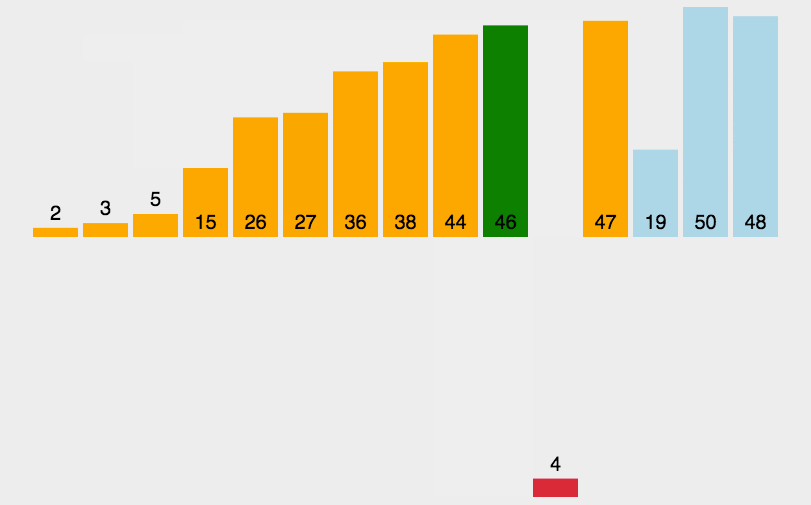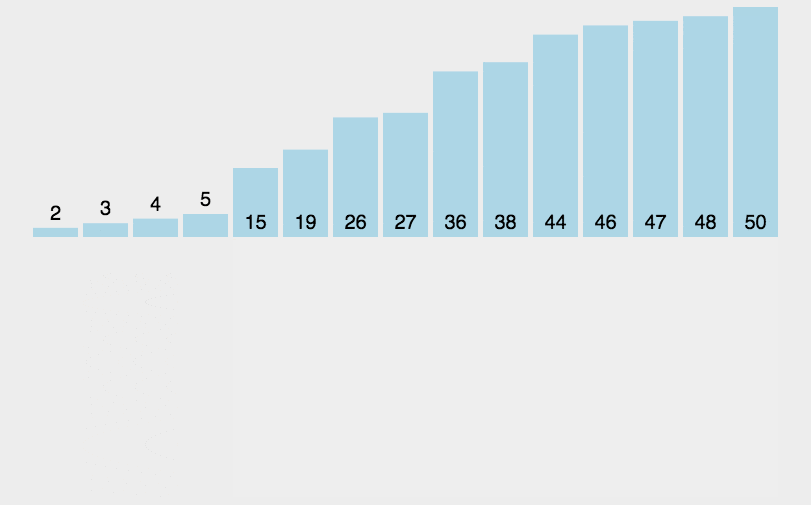
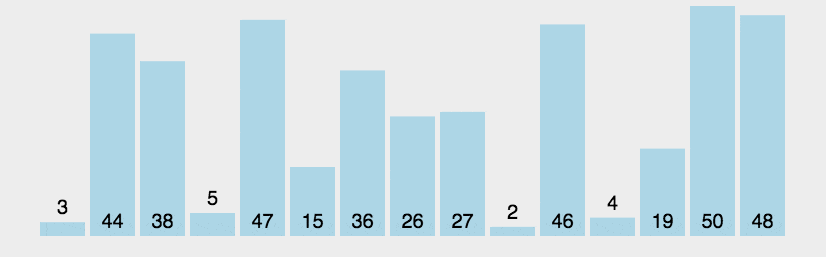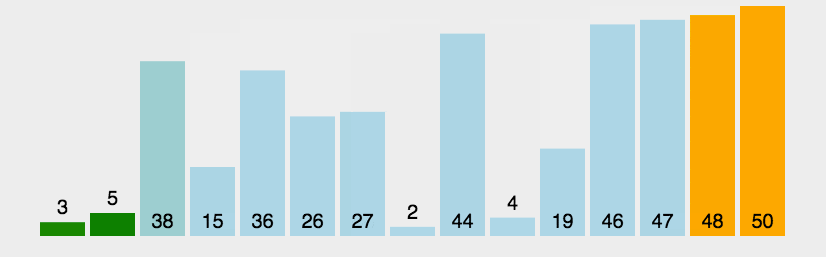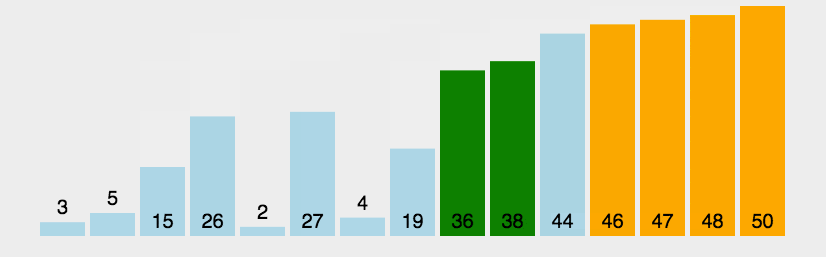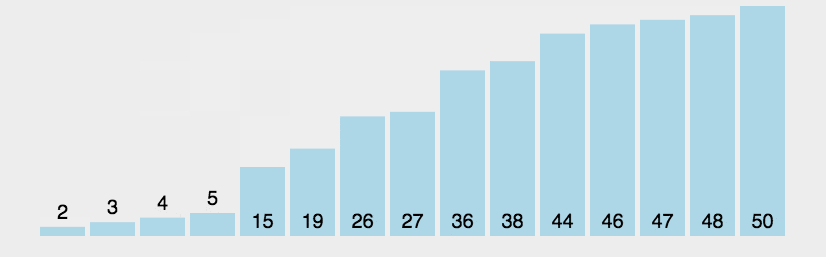前言

算是比较系统的重新学一遍算法，首先学算法，第一位接触的就是排序算法了。虽然很久以前用的就比较熟了，学习起来没什么难度。不过，通过看github那些大牛写的代码，同样受益匪浅，在一些代码处理上算是十分优秀了，也学到了一些测试方法——单元测试的AAA规则，Arrange,Act,Assert。同时还在自己编写修改代码时学上一些github工作流程，虽然只是学的毛皮，不过够用就行了。

排序算法上使用的API

所有排序算法的接口

public interface IComparisonSorter<T>
{
    /// <summary>
    ///     排序方法
    /// </summary>
    /// <param name="array">需要排序的数组</param>
    /// <param name="comparer">比较用的Comparer <paramref name="array" />.</param>
    void Sort(T[] array, IComparer<T> comparer);
}

comparer接口的比较规则

internal class IntComparer : IComparer<int>
{
    int IComparer<int>.Compare(int x, int y)
    {
        return x.CompareTo(y);
    }

    // public int Compare(int x, int y) => x.CompareTo(y);
}

冒泡排序

冒泡排序算是最简单的排序算法，两两进行比较交换直到不需要被交换

/// <summary>
///     冒泡排序类
/// </summary>
/// <typeparam name="T">数组元素类型</typeparam>
public class BubbleSorter<T> : IComparisonSorter<T>
{
    /// <summary>
    ///     时间复杂度 O(n^2)
    ///     空间复杂度 O(1)
    ///     在这里，我们按照升序排序
    ///     比较相邻元素，大的放在后面
    ///     这样子每次最后一个是最大元素
    ///     在不包含最大元素的范围重复步骤，直到没得交换
    ///     最好情况是 N - 1 次交换和 0 次交换
    ///     最坏情况是 N * (N - 1)/2 次交换
    /// </summary>
    /// <param name="array">要排序的数组</param>
    /// <param name="comparer">比较器</param>
    public void Sort(T[] array, IComparer<T> comparer)
    {
        for (var i = 0; i < array.Length - 1; i++)
        {
            var wasChanged = false;
            for (var j = 0; j < array.Length - i - 1; j++)
            {
                if (comparer.Compare(array[j], array[j + 1]) > 0)
                {
                    var temp = array[j];
                        array[j] = array[j + 1];
                    array[j + 1] = temp;
                    wasChanged = true;
                }
            }

            if (!wasChanged)
            {
                break;
            }
        }
    }
}

选择排序

选择排序也是特别简单的算法之一，即在未排序的找到最小（大）元素放在排序序列的起始位置，然后重复步骤。

namespace Algorithms.Sorters
{
    /// <summary>
    ///     实现选择排序的类
    /// </summary>
    /// <typeparam name="T">数组元素类型</typeparam>
    public class SelectionSorter<T> : IComparisonSorter<T>
    {
        /// <summary>
        ///     时间复杂度 O(n^2)
        ///     空间复杂度 O(1)
        ///     找到数组最小元素，然后和第一个位置交换
        ///     指针向后移动一位，然后再在剩下的数组元素找出最小
        ///     如此往复，总共进行了 N 次交换
        /// </summary>
        /// <param name="array">排序数组</param>
        /// <param name="comparer">比较器</param>
        public void Sort(T[] array, IComparer<T> comparer)
        {
            for (var i = 0; i < array.Length - 1; i++)
            {
                var jmin = i;
                for(var j = i + 1; j < array.Length; j++)
                {
                    if(comparer.Compare(array[jmin], array[j]) > 0)
                    {
                        jmin = j;
                    }
                }
                var temp = array[i];
                array[i] = array[jmin];
                array[jmin] = temp;
            }
        }
    }
}

插入排序

插入排序的工作原理就是从前往后扫描，将未排序的元素插入到已排序元素中。

namespace Algorithms.Sorters
{
    /// <summary>
    ///     实现插入排序的算法
    /// </summary>
    /// <typeparam name="T">数组元素类型</typeparam>
    public class InsertionSorter<T> : IComparisonSorter<T>
    {
        /// <summary>
        ///     时间复杂度 O(n^2)
        ///     空间复杂度 O(1)
        ///     我们保证当前需要排序的元素的前面是有序的
        ///     然后将该元素插入前面中
        ///     由于前面是有序的，假设是升序
        ///     只要找到第一个比它小的元素插入就停止
        ///     否则就一直两两交换位置直到第一位
        ///     平均情况下需要 N^2/4 次交换
        ///     最坏情况需要 N^2/2 次交换
        ///     最好情况需要 N - 1 次交换 和 0 次交换
        /// </summary>
        /// <param name="array">排序数组</param>
        /// <param name="comparer">比较器</param>
        public void Sort(T[] array, IComparer<T> comparer)
        {
            for (var i = 1; i < array.Length; i++)
            {
                for (var j = i; j > 0 && comparer.Compare(array[j], array[j - 1]) < 0; j--)
                {
                    var temp = array[j - 1];
                    array[j - 1] = array[j];
                    array[j] = temp;
                }
            }
        }
    }
}

希尔排序

希尔排序是优化过的插入排序，相对于插入排序只能一小步一小步的交换，希尔排序可以一大步一大步的交换，取决于当前的步长。

namespace Algorithms.Sorters
{
    /// <summary>
    ///     实现希尔排序的类
    /// </summary>
    /// <typeparam name="T">数组元素类型</typeparam>
    public class ShellSorter<T> : IComparisonSorter<T>
    {
        /// <summary>
        ///     希尔排序的最坏时间复杂度取决于step
        ///     在这里，我们使用比较普遍的 1,4,13,40 数列
        ///     若使用 对数组长度进行对半取，最坏时间复杂度大概为 O(n^2)
        ///     3*n+1 大概在 O(n^(3/2))
        ///     希尔排序就是用跳跃式的来减少最坏情况的发生
        ///     也就是说，原本插入可能要 N 次 交换，变到 3 次交换
        ///     最优的最坏时间复杂度为O(n*(logn)^2),但是step的计算比较麻烦
        ///     所以通常用 3 为倍数
        /// </summary>
        /// <param name="array">排序数组</param>
        /// <param name="comparer">比较器</param>
        public void Sort(T[] array, IComparer<T> comparer)
        {
            var step = 1;
            while (step < array.Length / 3) step = 3 * step + 1;
            while (step >= 1)
            {
                GappedInsertionSort(array, comparer, step);
                step /= 3;
            }
        }

        private static void GappedInsertionSort(T[] array, IComparer<T> comparer, int step)
        {
            for (var i = step; i < array.Length; i++)
            {
                for (var j = i; j >= step && comparer.Compare(array[j], array[j - step]) < 0; j -= step)
                {
                    var temp = array[j];
                    array[j] = array[j - step];
                    array[j - step] = temp;
                }
            }
        }
    }
}

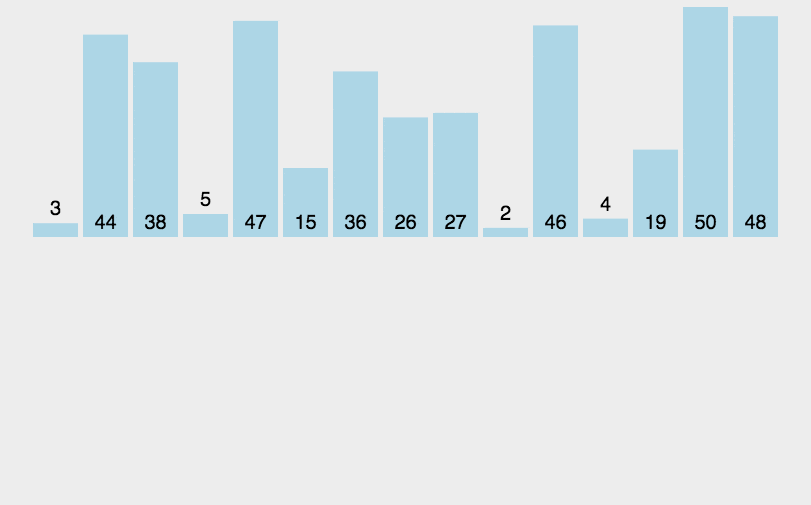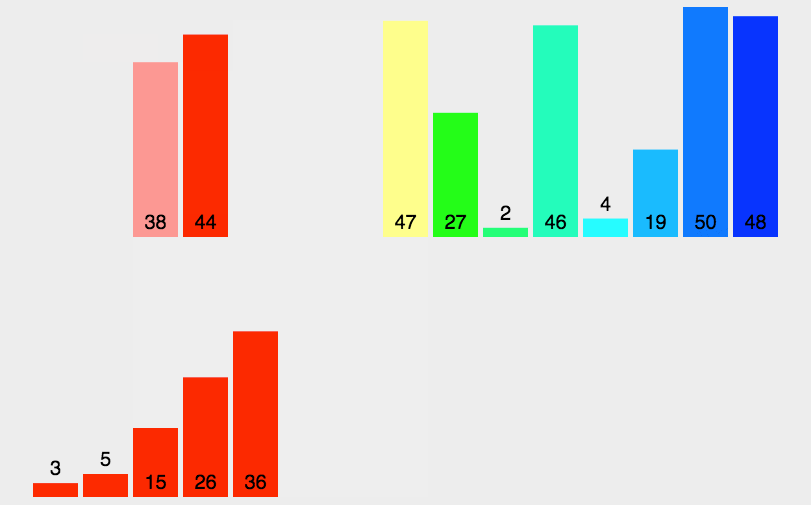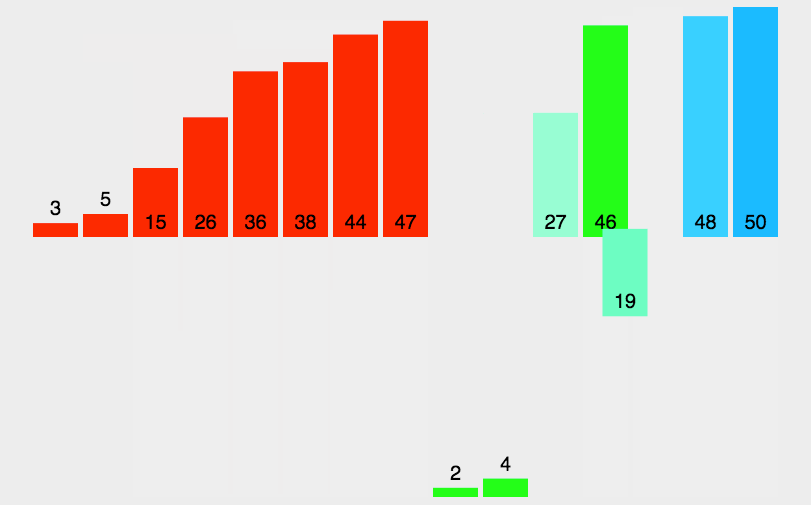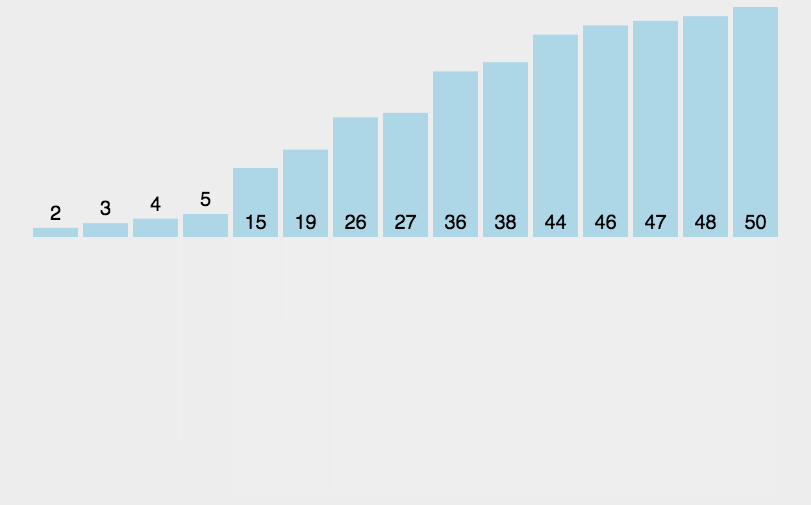
归并排序

namespace Algorithms.Sorters
{
    /// <summary>
    ///     实现归并排序的类
    /// </summary>
    /// <typeparam name="T">数组参数类型</typeparam>
    public class MergeSorter<T> : IComparisonSorter<T>
    {
        /// <summary>
        ///     时间复杂度 O(n*logn)
        ///     空间复杂度 O(n)
        ///     归并数组就是将两个有序的数组归并成更大的有序数组
        ///     通常用自顶向下比较容易理解
        ///     不断递归到大小只有 1 的数组，然后逐步向上归并
        /// </summary>
        /// <param name="array"></param>
        /// <param name="comparer"></param>
        public void Sort(T[] array, IComparer<T> comparer)
        {
            if (array.Length <= 1)
            {
                return;
            }

            var (left, right) = Split(array);
            Sort(left, comparer);
            Sort(right, comparer);
            Merge(array, left, right, comparer);
        }

        private static void Merge(T[] array, T[] left, T[] right, IComparer<T> comparer)
        {
            var mainIndex = 0;
            var leftIndex = 0;
            var rightIndex = 0;

            while (leftIndex < left.Length && rightIndex < right.Length)
            {
                var compResult = comparer.Compare(left[leftIndex], right[rightIndex]);
                array[mainIndex++] = compResult <= 0 ? left[leftIndex++] : right[rightIndex++];
            }

            while (leftIndex < left.Length)
            {
                array[mainIndex++] = left[leftIndex++];
            }

            while (rightIndex < right.Length)
            {
                array[mainIndex++] = right[rightIndex++];
            }
        }

        private static (T[] left, T[] right) Split(T[] array)
        {
            var mid = array.Length / 2;
            return (array.Take(mid).ToArray(), array.Skip(mid).ToArray());
        }
    }
}

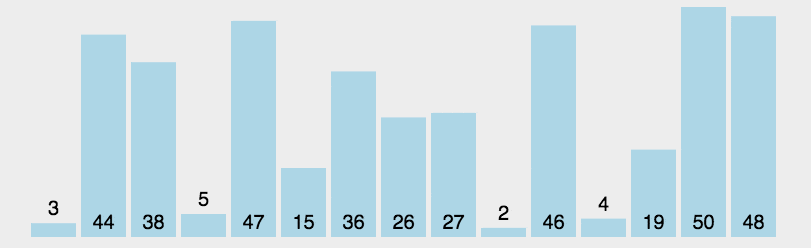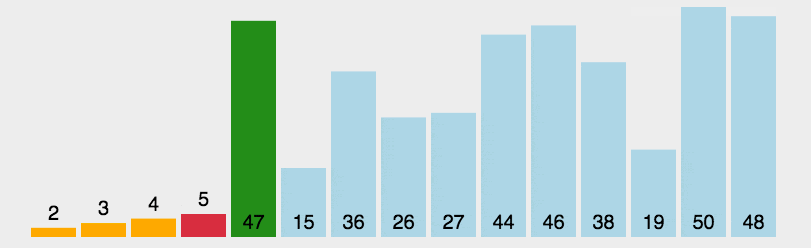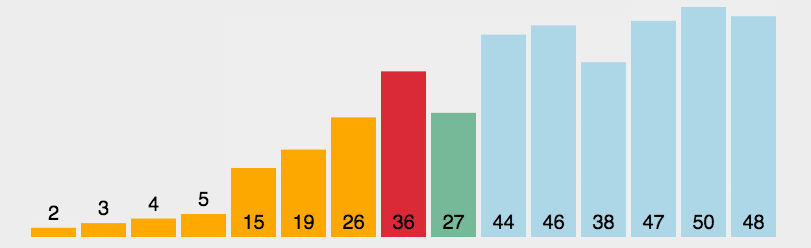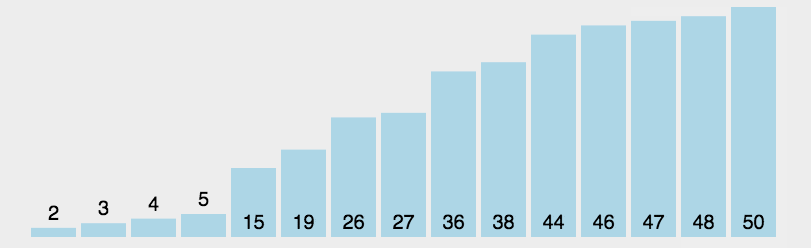
快速排序

namespace Algorithms.Sorters
{
    /// <summary>
    ///     实现快速排序的类
    /// </summary>
    /// <typeparam name="T"></typeparam>
    public abstract class QuickSorter<T> : IComparisonSorter<T>
    {
        /// <summary>
        ///     平均时间复杂度 O(nlogn)
        ///     最坏情况下时间复杂度 O(n^2)
        ///     空间复杂度 O(logn)
        ///     选定一个参数，将比它小的数放左边，比它大的数放右边  
        /// 
        /// </summary>
        /// <param name="array"></param>
        /// <param name="comparer"></param>
        public void Sort(T[] array, IComparer<T> comparer) => Sort(array, comparer, 0, array.Length - 1);

        protected abstract T SelectPivot(T[] array, IComparer<T> comparer, int left, int right);

        private void Sort(T[] array, IComparer<T> comparer, int left, int right)
        {
            if (left >= right)
            {
                return;
            }
            var mid = Partition(array, comparer, left, right);
            Sort(array, comparer, left, mid);
            Sort(array, comparer, mid + 1, right);
        }

        private int Partition(T[] array, IComparer<T> comparer, int left, int right)
        {
            var pivot = SelectPivot(array, comparer, left, right);
            var nleft = left;
            var nright = right;
            while (true)
            {
                while (comparer.Compare(array[nleft], pivot) < 0)
                {
                    nleft++;
                }
                while (comparer.Compare(array[nright], pivot) > 0)
                {
                    nright--;
                }

                if (nleft >= nright)
                {
                    return nright;
                }

                var temp = array[nleft];
                array[nleft] = array[nright];
                array[nright] = temp;

                nleft++;
                nright--;
            }
        }
    }
}

随便选一位参数

namespace Algorithms.Sorters
{
    /// <summary>
    ///     随便选一个作为参数进行快排
    /// </summary>
    /// <typeparam name="T"></typeparam>
    public sealed class RandomPivotQuickSorter<T> : QuickSorter<T>
    {
        private readonly Random _random = new();
        protected override T SelectPivot(T[] array, IComparer<T> comparer, int left, int right)
            => array[_random.Next(left, right + 1)];
    }
}

选中间为参数

namespace Algorithms.Sorters
{
    /// <summary>
    ///     以数组中间为参数，进行快排
    /// </summary>
    /// <typeparam name="T"></typeparam>
    public sealed class MiddlePointQuickSorter<T> : QuickSorter<T>
    {
        protected override T SelectPivot(T[] array, IComparer<T> comparer, int left, int right)
            => array[left + (right - left) / 2];
    }
}

三向切分快速排序

namespace Algorithms.Sorters
{
    /// <summary>
    ///     实现三向切分快排的类
    /// </summary>
    /// <typeparam name="T"></typeparam>
    public class Quick3waySorter<T> : IComparisonSorter<T>
    {
        /// <summary>
        ///     时间复杂度与快排差不多
        ///     但是对大量重复元素执行效率更高
        ///     在快排的基础上，我们选一个参数
        ///     但是有重复元素，我们将重复元素放在中间
        ///     然后对左对右进行分别递归
        ///     这样子减少对重复的排序
        /// </summary>
        /// <param name="array"></param>
        /// <param name="comparer"></param>
        public void Sort(T[] array, IComparer<T> comparer)
            => Sort(array, comparer, 0, array.Length - 1);
        private void Sort(T[] array, IComparer<T> comparer, int left, int right)
        {
            if (left >= right)
            {
                return;
            }

            var (lt, rt) = Partition(array, comparer, left, right);
            Sort(array, comparer, left, lt - 1);
            Sort(array, comparer, rt + 1, right);
        }

        private (int lt, int rt) Partition(T[] array, IComparer<T> comparer, int left, int right)
        {
            var pivot = array[left];
            var lt = left;
            var i = left + 1;
            var rt = right;

            while (i <= rt)
            {

                var cmp = comparer.Compare(array[i], pivot);
                if (cmp < 0)
                {
                    Swap(array, lt++, i++);
                }
                else if (cmp > 0)
                {
                    Swap(array, i, rt--);
                }
                else
                {
                    i++;
                }
            }

            return (lt, rt);
        }

        private void Swap(T[] array, int x, int y)
        {
            var temp = array[x];
            array[x] = array[y];
            array[y] = temp;
        }
    }
}

堆排序

堆排序即是利用堆的特性来进行排序，得出得结果是让数组为一个大根堆数组，而不是有序数组，若要获得有序数组，需要将堆顶一个一个拿出来，拿出堆顶时间为O(1)，维护剩余的堆需要logn，所以总的时间复杂度为nlogn

namespace Algorithms.Sorters
{
    /// <summary>
    ///     实现堆排序的类 这里是小根堆
    /// </summary>
    /// <typeparam name="T">数组元素类型</typeparam>
    public class HeapSorter<T> : IComparisonSorter<T>
    {
        /// <summary>
        ///     时间复杂度 O(nlogn)
        /// </summary>
        /// <param name="array"></param>
        /// <param name="comparer"></param>
        public void Sort(T[] array, IComparer<T> comparer)
            => HeapSort(array, comparer);

        private static void HeapSort(IList<T> data, IComparer<T> comparer)
        {
            // 创建堆？
            var heapSize = data.Count;
            for (var p = (heapSize - 1) / 2; p >= 0; p--)
            {
                  MakeHeap(data, heapSize, p, comparer);
            }

            // 将降序堆转化为升序队列，即将每个大根堆堆顶的元素取走然后重塑堆
            for (var i = data.Count - 1; i >= 0; i--)
            {
                var temp = data[i];
                data[i] = data[0];
                data[0] = temp;

                heapSize--;
                MakeHeap(data, heapSize, 0, comparer);
            }
        }

        private static void MakeHeap(IList<T> data, int heapSize, int index, IComparer<T> comparer)
        {
            var largest = index;
            var left = 2 * (index + 1) - 1;
            var right = 2 * (index + 1);

            if (left < heapSize && comparer.Compare(data[left], data[largest]) > 0)
            {
                largest = left;
            }

            if (right < heapSize && comparer.Compare(data[right], data[largest]) > 0)
            {
                largest = right;
            }

            if (largest != index)
            {
                var temp = data[index];
                data[index] = data[largest];
                data[largest] = temp;

                MakeHeap(data, heapSize, largest, comparer);
            }
        }
    }
}

总结

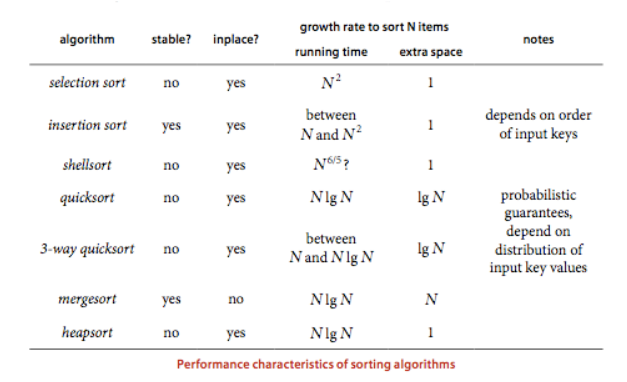
可以直白的说，大多数情况下，快速排序是最佳选择。我们在工程实践上通常用的是官方提供的库，除非是要写的语言没有提供官方库，或者是官方库的算法不太理想，才会去自己手写排序。