图形学 几何变换

前言

最近在复习图形学理论知识，顺便补一下记录，在这里记录的是比较常见的变换，会有一些比较复杂的地方没有涉及到。在图形学的变换中，对于数学的要求并不是很高，只需要会简单的线性代数矩阵乘法即可。

2D线性变换(Linear Transformation)

我们将点坐标以向量作为表示，变换以矩阵表示。两者相乘就是点经过变换后的新位置

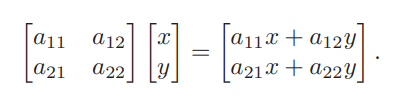
缩放变换(Scaling)

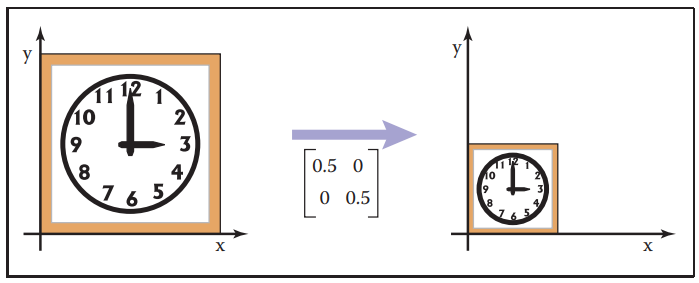
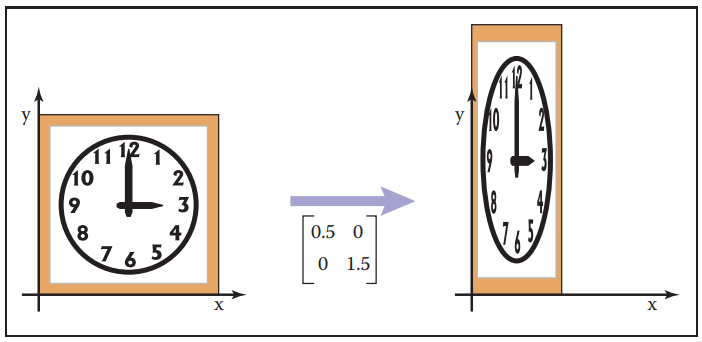
缩放变换就是原坐标乘以一个数进行变换,设原点为(x,y),新点为(sx * x, sy * y),可以很快反推出矩阵。

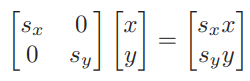
剪切变换(Shearing)

不知道该怎么翻译，应该是将正方形变形为平行四边形的操作。

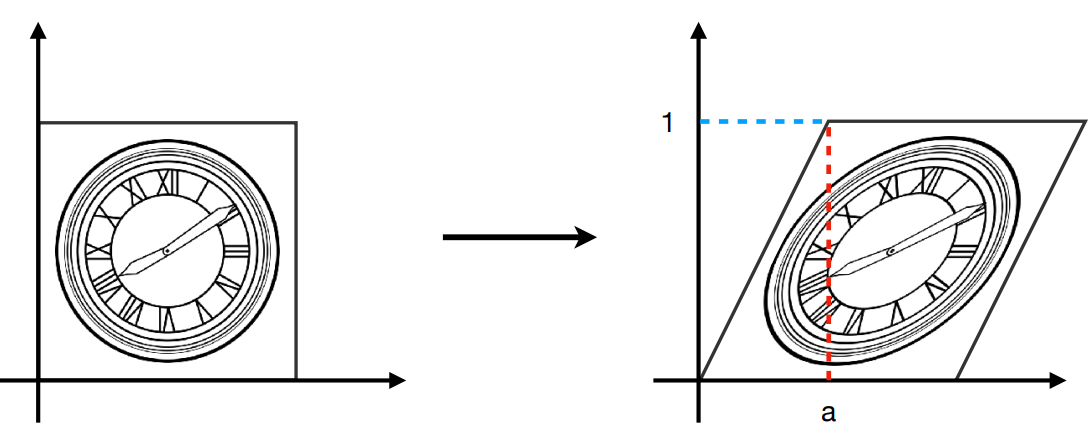
假设只对x进行变换，而不对y进行变换，那么x新坐标即为(1+ay)，稍微反推一下，获取关键坐标(0,0) (a,1),y 没有进行剪切变换。

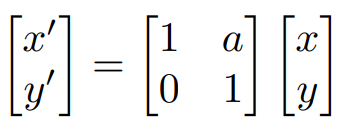
另一种方法可以想为shearing只是对一个轴进行旋转一个角度

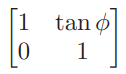
旋转变换(Rotation)

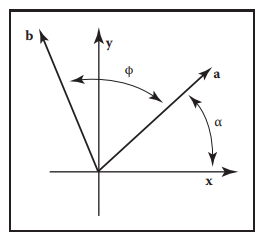
假设点a到(0,0)距离为r，那么xa = rcosα, ya = rsinα所示，我们将a向量旋转到b向量，那么

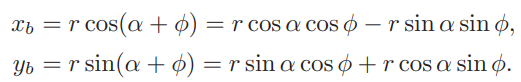
将xa = rcosα, ya = rsinα带入后得到

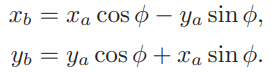
然后我们推出旋转矩阵为

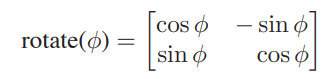
以上是逆时针旋转的矩阵

对称变换(Reflection)

其实跟缩放变换差不多

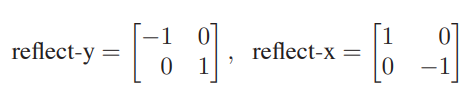
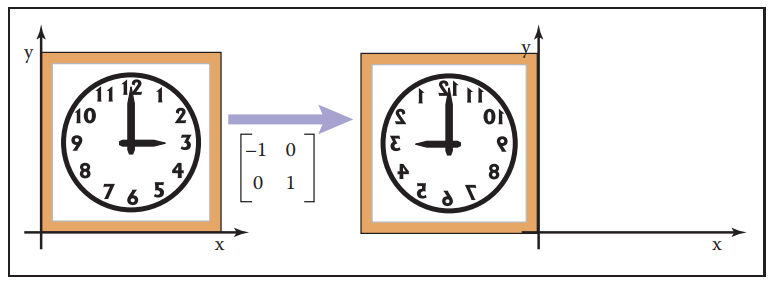
变换的组合

由于矩阵乘法一般不满足交换律，即 AB != BA,所以变换的顺序比较重要

3D线性变换

scaling

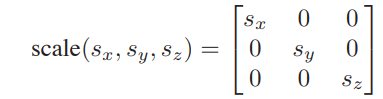
rotation

旋转较二维有所不同，我们只需要了解对应不同轴旋转的矩阵

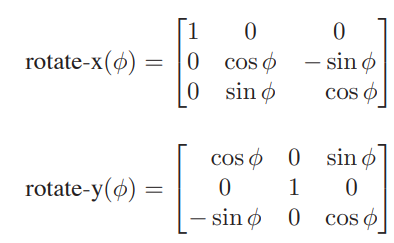
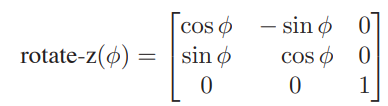
绕任意轴旋转：我们只有绕x，y，z旋转的方法，我们将轴给旋转到x/y/z上，然后再应用标准旋转矩阵，最后将轴逆旋转回到原先的地方就完成了

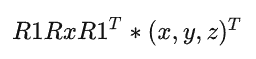
接下来我们尝试将将u v w(已知u，任取t方向与u组成平面，利用叉乘特性得到v w) 对应到 x y z

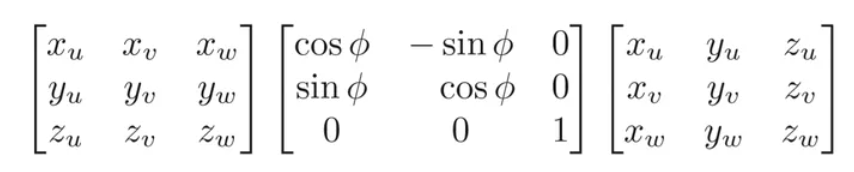
仿射变换(affine transformation)

前面一直在讨论线性变换，也就是依据原点(0,0)进行变换，如果我们加上位置变换(Translation)就会让之前的所有矩阵都不成立。为了相同，我们增加一维，让(x,y) -> (x,y,1) 这样子当 x’ = m11x + m12y + xt时，就不会打乱之前的线性变换矩阵。

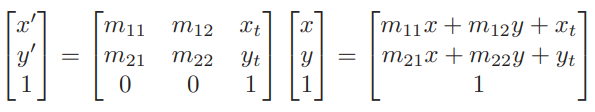
这样子的向量是不是很熟悉，也就是齐次坐标，最后一维为1是一个坐标，为0时是一个向量，对于其他数字，我们要将坐标进行归一化，也就是(x,y,w) -> (x/w,y/w,1)

在三维状态下也是如此

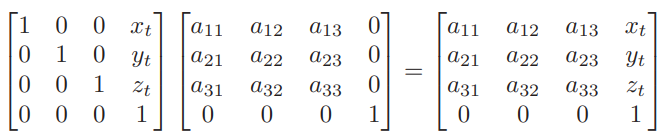
视图变换(Viewing Transformation)

在之前的变换，我们讨论了如何变换点的位置。现在我们要将现实世界中的点投影在屏幕上，我们将要经历三步

  • 摄像机变换(eye/camera transformation) : 调整摄像机位置，旋转角度，也就是得到物体与摄像机的相对位置
  • 投影变换(projection transformation) : 摄像机变换后，得到可视范围物体对于摄像机的相对坐标，之后根据情况选择平行投影或者透视头型，将三维空间投影至标准二维平面[-1,1]^2
  • 视口变换(viewport transformatino) ： 将[-1,1]^2 -> [0,width][0,height],也就是*将标准平面映射到屏幕分辨率范围上

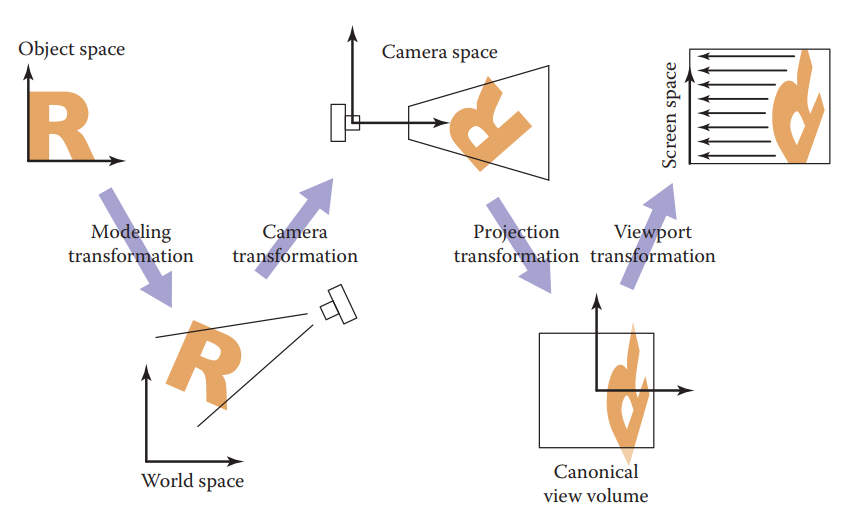
视口变换

先从视口变换入手，视口变换是最简单也是最容易理解的矩阵，将-1 -> 0 ,1 - > width/height 也就是简单的缩放变换，然后为了保持原点在屏幕中间，多了一步Translation

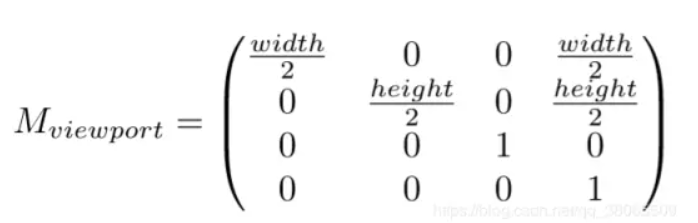
正交（Orthographic）投影变换

正交投影也是简单的缩放变换和位移，我们用一个包围盒围住物体，要注意的是在这里，n > f，因为我们是从-z往物体上看的

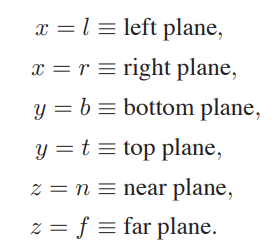
由于是空间的变换，容易得到以下矩阵
证明过程，先举一个二维的例子：

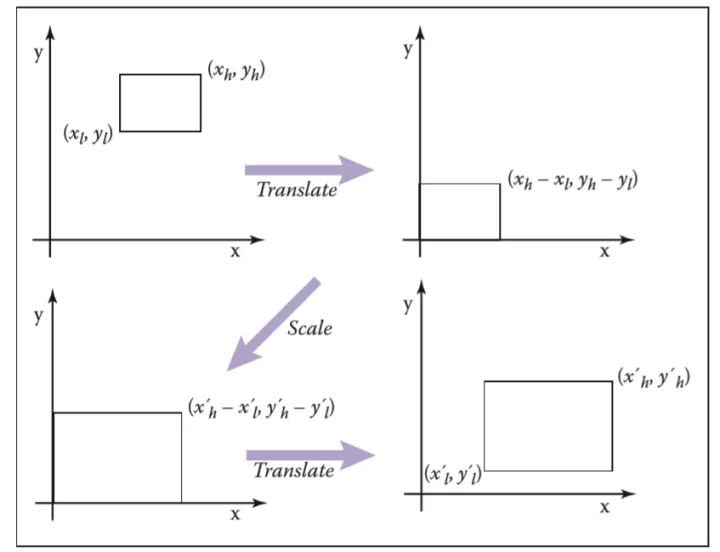
可以发现分三步走，Translate（移动到原点）->Scale（进行缩放变化）->Translate（移动到对应的位置）

推广到三维

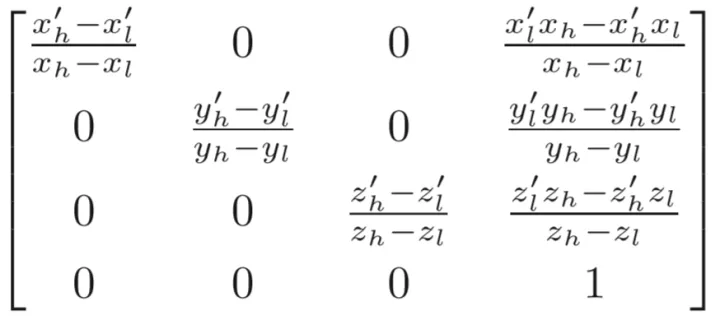
将[l, r] [t, b] [n, f] 和 [-1, 1]^3 代入得正交矩阵

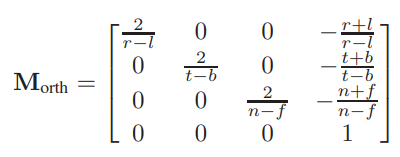
摄像机变换

虽然说是摄像机变换，但其实是调整物体的位置，将摄像机的坐标轴对应到原世界的x，y，z就行了，问题就变成了将camera的坐标系变到与原世界坐标系重合

我们先定义摄像机的三个属性

  • e(eye position) : 摄像机位置
  • g(gaze direction) : 摄像机朝向的角度
  • t(view-up vector) : 摄像机朝向角度的正上方向，也就是为了g，t组成一个平面

然后我们得到摄像机坐标系

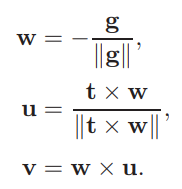
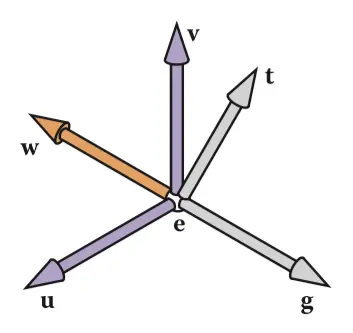
我们将摄像机变换分成两步

  • 移动到原点
  • 通过旋转矩阵将二者坐标系重合

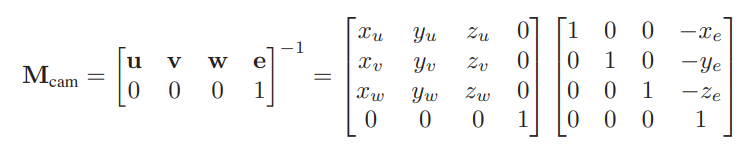
透视投影变换

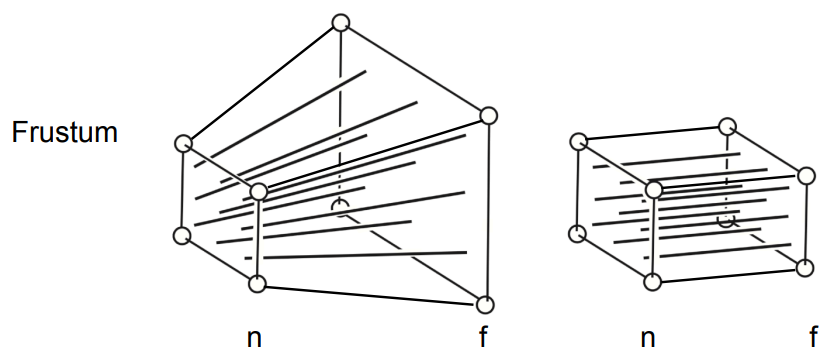
透视变换就是将原本的包围盒变成一个具有近大远小属性的锥形盒子

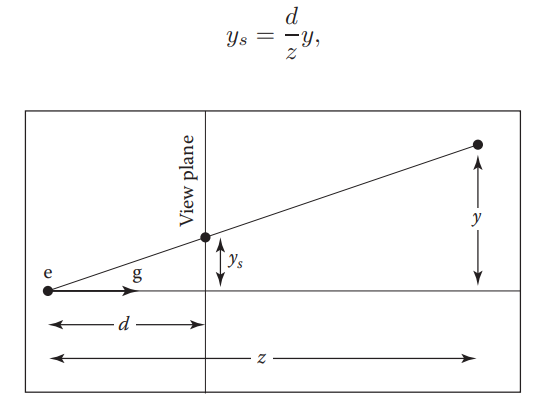
我们容易得到以下对应关系，但是第三行如何得出，利用近平面和远平面的z坐标不变的性质进行代入

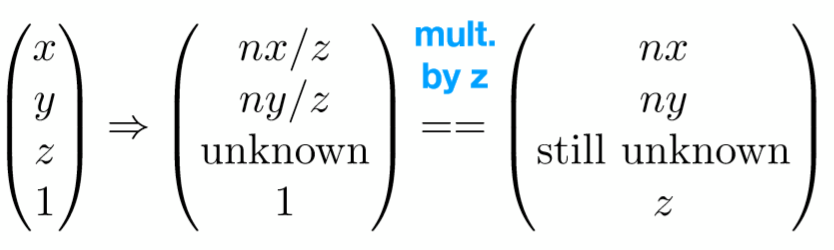
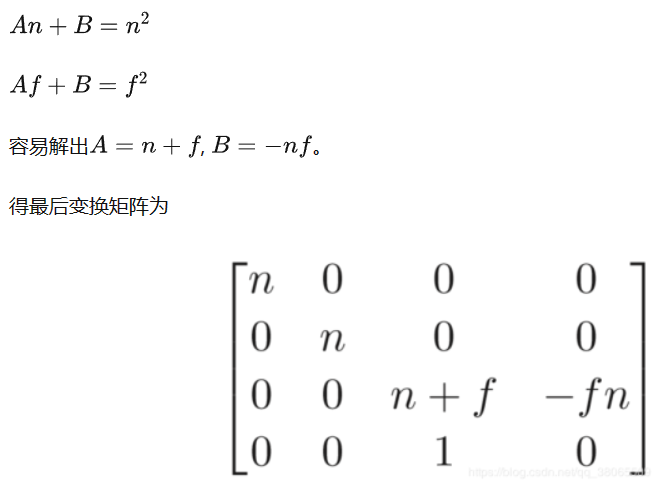
现在我们已经得到了包围盒变为锥形盒子的矩阵 P
可以很快得到一个等式 Mper = Morth * P
也就是说，我们先将包围盒变成 [-1,1] ^ 2 的，然后在这个[-1,1] ^ 2的小正方体进行透视变换，这与先变为锥形盒子再压缩到[-1,1] ^ 2是一样的,得出以下矩阵

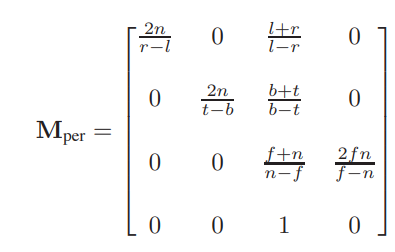
简短的总结

我们在经历过上述计算后，可以得出现实世界到屏幕上的矩阵变换 M = Mview * Mper * Mcam * Mmodel

参考