前言
系统的学习完图形学发现还有一些小细节有所疏漏,在此记录
变换法线向量
法线变换矩阵
为了进行光照计算,一般要使用到模型的顶点的法线进行计算。局部坐标经过矩阵M转化到世界坐标,然后再通过矩阵V转化到观察空间。则观察空间的顶点位置则变为MVp(顶点坐标),而顶点法线却不能直接直接由MVn(顶点法线)计算,因为模型发生non-uniform缩放时,经过MVn变换后的法线不在与模型表面垂直。
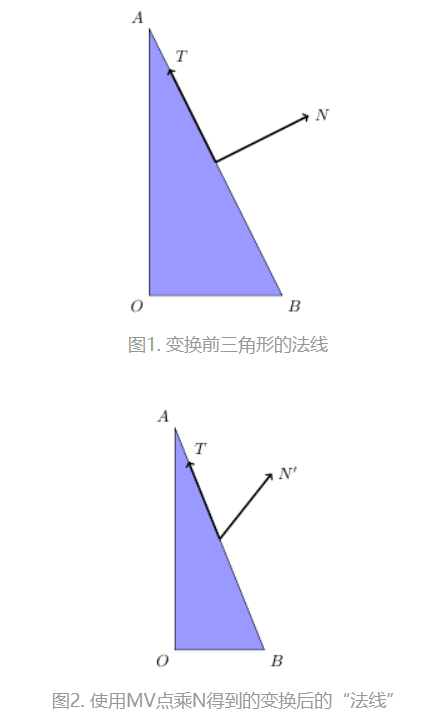
用于法线变换的矩阵应该是:
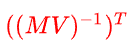
如果是在世界坐标上计算,则法线变换的矩阵为
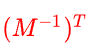
推导过程
我们设T为切向向量,N为法线向量,P2,P1为三角形边上的某两个点,带’的变量为变换后的坐标
-> T = P2 - P1
-> MVT = MV(P2-P1)
-> MVT = MVP2 - MVP1
从而得到 T’ = P2’ - P1’
因为切线向量和法线向量永远垂直,所以TN = 0
设N’ = G * N(G为我们要解出的法线变换矩阵)
-> N’T’ = (GN)(MVT) = 0
由于GN时列向量,所以做点积时要转置成行向量
-> (GN)^转置 * (MVT) = N^转置 G^转置 MVT = 0
为了让N^转置 *T = 0 则 G^转置MV = I(单位矩阵)
-> G = ((MV)^-1)^转置
参考
透视矫正插值
原因
我们的重心坐标往往都是在屏幕空间下得到的,如果使用屏幕空间下的重心坐标进行插值会造成一定的误差,与在观察空间时不一样的。因为到了屏幕空间,插值运算就不会考虑近大远小了。
推导


我们对A,B点画x轴方向的线交于OC

易得(t/1-t) = AG/BK = (acZ1/d)/(bcZ2/d) = sZ1/(1-m)/Z2 ,对两边用倒数进行处理得到
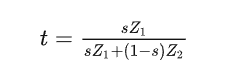
再将该式子代入(6)得
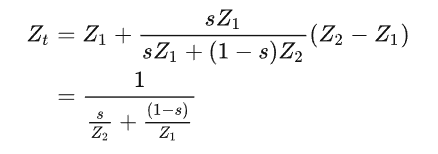
上述是两个点的计算,推广到重心坐标,得
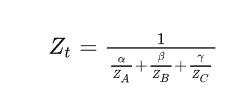
然后进行推广到任意属性(法线向量,纹理坐标等)
