LRU & TopK

LRU

最近最少使用(Least Recently Used) ，加入新的将最少使用的元素淘汰掉

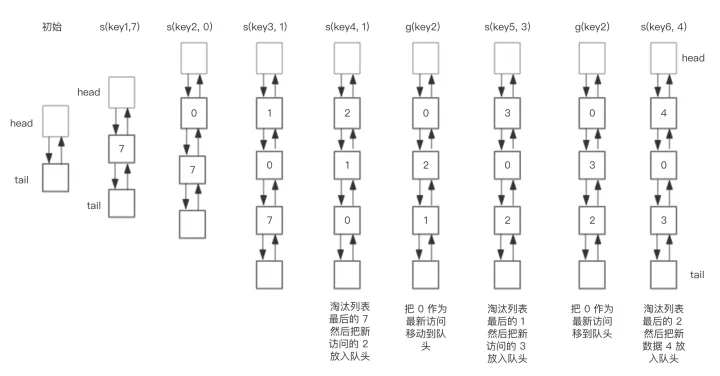
两种操作：

• 当访问时，如果有就将访问的挪到头
• 当加入时，将新的挪到头，如果链表满了，将尾移除

O(1)操作头尾元素，用双向链表，O(1)时间访问用哈希表

手搓双向链表实现:

class LRUCache {
public:
    struct DLNode{
        int key,value;
        DLNode* prev,*post;
        DLNode(int k, int v): key(k),value(v),prev(nullptr),post(nullptr){}
    }*head,*tail;

    int capacity;
    unordered_map<int,DLNode*> hashmap;

    LRUCache(int capacity):capacity(capacity) {
        head = new DLNode(-1,-1);
        tail = new DLNode(-1,-1);
        head->post = tail;
        tail->prev = head;
    }
    
    void remove(DLNode* cur)
    {
        cur->post->prev = cur->prev;
        cur->prev->post = cur->post;
    }
    void insert(DLNode* cur)
    {
        cur->post = head->post;
        cur->prev = head;
        head->post->prev = cur;
        head->post = cur;
    }
    int get(int key) {
        if(hashmap.count(key) == 0) return -1;
        auto cur = hashmap[key];
        remove(cur);
        insert(cur);
        return cur->value;
    }
    
    void put(int key, int value) {
        if(hashmap.count(key) > 0)
        {
            auto cur = hashmap[key];
            cur->value = value;
            remove(cur);
            insert(cur);
        }
        else 
        {
            if(hashmap.size() == capacity)
            {
                auto leastUse = tail->prev;
                remove(leastUse);
                hashmap.erase(leastUse->key);
                delete leastUse;
            }
            auto cur = new DLNode(key,value);
            hashmap[key] = cur;
            insert(cur);
        }
    }
};

优雅的STL版本:

class LRUCache {
public:
    LRUCache(int capacity): capacity(capacity) {

    }
    
    int get(int key) {
        if(map.find(key) == map.end()) return -1;
        auto key_value = *map[key];
        cache.erase(map[key]);
        cache.push_front(key_value);
        map[key] = cache.begin();
        return key_value.second;
    }
    
    void put(int key, int value) {
        if(map.find(key) != map.end()) cache.erase(map[key]);
        else if(cache.size() == capacity)
        {
            map.erase(cache.back().first);
            cache.pop_back();
        }
        cache.push_front({key,value});
        map[key] = cache.begin();
    }
private:
    int capacity;
    list<pair<int,int>> cache;
    unordered_map<int,list<pair<int,int>>::iterator> map;
};

TopK

字面意思，就是求无序数组的第k大的数

最大值最小值

先从寻找最大值最小值开始，直接遍历也就是O(n)的时间复杂度。

伪代码：

min = A[1]
for i = 2 to A.length 
    if min > A[i] min = A[i]

# 上述伪代码一眼O(n)
# 如果求同时最大最小值，可以稍微优化一下，从每个数与min 和 max 比较，总共一轮是两次的比较，优化到3/2次比较

min = A[1] vs A[2] 
max = A[1] vs A[2]
for i = 3 to A.length 
    if(A[i] < A[i + 1])
        if(min > A[i]) min = A[i]
        if(max < A[i + 1]) max = A[i + 1]
    else 
        ...
    i += 2

# 这样子成对处理就会优化到总共 3n/2 - 2 次比较

TopK

• 在这里我们找第 k 小的数
• 利用快速排序的partition思想
• 当partition分出来的 i < k 时，也就是我们找到第 i 小的数，我们需要在 i + 1 ~ n中找第k小的数。当 i > k 时，我们需要在 1 ~ i - 1中找第k小的数。
• 如果 i == k 说明刚好找到
• partition 的思想就是让 i 左边的数都小于 i 右边的数都大于 i ，不care i 左右两边内部的顺序，只care i 的位置。

期望时间复杂度为O(n)，假设每次都是刚好分半, 有可能还更小 T(n) + T(n/2) + T(n/4) +… T(1) 也就是等积数列求和为 T(2n) 所以为O(n)

最坏情况为O(n^2)，如果很不幸每次都是找到一组的最大元素进行partition 就会造成 T(n) + T(n - 1) + T(n - 2) + .. T(1) 的情况 最后为T(n^2),所以用random划分来尽可能地避免该情况

伪代码:算法导论中第七章的快排的partition十分优雅，可以看看

#include <iostream>
#include <vector>

int RandomPartition(std::vector<int> &nums, int l, int r)
{
    int q = rand()%(r - l + 1) + l;
    std::swap(nums[q],nums[r]);
    auto x = nums[r];
    int i = l - 1;
    for (int j = l; j < r; ++j)
    {
        if (nums[j] <= x)
            std::swap(nums[++i], nums[j]);
    }
    std::swap(nums[i + 1], nums[r]);
    return i;
}

int TopK(std::vector<int> &nums, int l, int r, int k)
{
    int i = RandomPartition(nums, l, r);
    if (i == k)
        return nums[i];
    else
        return i < k ? TopK(nums, i + 1, r, k) : TopK(nums, l, i - 1, k);
}
int main()
{
    srand(time(0));
    std::vector<int> nums{2, 8, 7, 1, 3, 5, 6, 4};

    int ans = TopK(nums, 0, nums.size() - 1, 3);
    std::cout << ans;
    return 0;
}