TSP

简介

TSP全称为Travelling Salesman Problem（旅行商问题），通俗而言，它是指对于给定的一系列城市和每对城市之间的距离，找到访问每一座城市仅一次并回到起始城市的最短回路。
由于求精确解的时间复杂度很大，衍生出了很多近似算法，不过在这里不讨论，我们在这里只讨论精确解DP算法

  • 有n个城市，从起点 0 开始游历每一个城市，只访问每个城市一次，最后回到起点，所需要的最短路径是多少？
  • 定义dp[S][i] ,S为集合即已经走过的城市，但是从0个城市到所有城市的集合太多了，所以我们采用状态压缩，便于遍历。dp[S][i] 即在i点结束，集合S中每个点恰好走过一次时的最短路长度
  • 所以最终答案是 min(dp[S][i]),S为所有城市，i的话每个点都可能是终点。

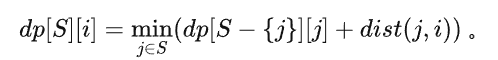
容易得出以上状态转移方程，即dp[S][i] = min(不包括 i 的集合 + j 到 i 的距离)
上图有些错误，应该是 dp[S-{i}] ,下面看代码

参考代码，模板：

#include <iostream>
#include <vector>

using namespace std;

const int n = 4;

int d[n][n] = {
    {0, 10, 15, 20},
    {10, 0, 25, 25},
    {15, 25, 0, 30},
    {20, 25, 30, 0},
};

int main()
{
    int minn = INT_MAX;
    vector<vector<int>> dp(1 << n, vector<int>(n));

    for (int nowstate = 1; nowstate < (1 << n); ++nowstate) // 集合变化
    {
        dp[nowstate] = vector<int>(n, INT_MAX);// 初始化dp数组
        for (int j = 0; j < n; ++j)
        {
            if ((nowstate & (1 << j))) // 如果现在的状态包括 j 这个城市
            {
                int preState = nowstate ^ (1 << j);
                if (preState == 0) // 如果集合只包括 j 这个城市 那么dp值为 d[0][j] 假设起点是0的话
                    dp[nowstate][j] = d[0][j];
                else // 集合不止 j 这个城市 , 遍历 0 ~ n 城市，如果前置状态也就是 S - {j} 这个集合都没更新的话就不用理了，如果更新了就进行比较
                {
                    for (int i = 0; i < n; ++i)
                    {
                        if (dp[preState][i] < INT_MAX && dp[preState][i] + d[i][j] < dp[nowstate][j])
                            dp[nowstate][j] = dp[preState][i] + d[i][j];
                    }
                }
            }
        }
    }
    for (int j = 0; j < n; ++j)
        minn = min(minn, dp[(1 << n) - 1][j] + d[0][j]); // 如果是要求环就加上 d[0][j] 如果不是的话就不用加
    cout << minn << endl;
    return 0;
}

943.最短超级串:

#include <iostream>
#include <string>
#include <vector>
#include <stack>
#include <bitset>
using namespace std;

int calu(const string &a, const string &b);

string shortestSuperstring(vector<string> &words)
{
    int n = words.size();

    vector<vector<int>> graph(n, vector<int>(n));

    for (int i = 0; i < n; ++i)
    {
        for (int j = 0; j < i; ++j)
        {
            graph[i][j] = calu(words[i], words[j]);
            graph[j][i] = calu(words[j], words[i]);
        }
    }

    vector<vector<int>> dp(1 << n, vector<int>(n));
    vector<vector<int>> path(1 << n, vector<int>(n));

    for (int now_state = 1; now_state < (1 << n); ++now_state)
    {
        dp[now_state] = vector<int>(n, INT_MAX);

        for (int j = 0; j < n; ++j)
        {
            if ((now_state & (1 << j)) > 0)
            {
                int pre_state = now_state ^ (1 << j);
                if (pre_state == 0)
                    dp[now_state][j] = words[j].size();
                else
                {
                    for (int i = 0; i < n; ++i)
                    {
                        if (dp[pre_state][i] < INT_MAX && dp[pre_state][i] + graph[i][j] < dp[now_state][j])
                        {
                            dp[now_state][j] = dp[pre_state][i] + graph[i][j];
                            path[now_state][j] = i;
                        }
                    }
                }
            }
        }
    }

    int last = -1, minn = INT_MAX;
    for (int i = (1 << n) - 1, j = 0; j < n; ++j)
    {
        if (dp[i][j] < minn)
        {
            minn = dp[i][j];
            last = j;
        }
    }

    int cur = (1 << n) - 1;
    stack<int> s;
    while (cur > 0)
    {
        s.push(last);
        int temp = cur;
        cur ^= (1 << last);
        last = path[temp][last];
    }

    string result = "";
    int i = s.top();
    s.pop();
    result += words[i];
    while (!s.empty())
    {
        int j = s.top();
        s.pop();
        result += (words[j].substr(words[j].size() - graph[i][j]));
        i = j;
    }
    return result;
}

int calu(const string &a, const string &b)
{
    for (int i = 0; i < a.size(); ++i)
        if (b.rfind(a.substr(i), 0) == 0)
            return b.size() - (a.size() - i);

    return b.size();
}

int main()
{
    vector<string> words{"ab", "a", "b"};

    cout << shortestSuperstring(words);

    return 0;
}

参考