Fast Fibonacci

TalentStream

2024-01-07

Introduction:

本文将探讨一些踩坑点和算法的实现，并不会探讨 Fibonacci 为何，及如何推导公式。

F(n) = F(n - 1) + F(n - 2):

这算是最容易想到的算法了，时间复杂度为$O(n)$, 用递归空间复杂度会到$O(n)$, 递推会优化到$O(1)$ 。

<<Recursive Function>>
int Recursive(int n)
{
    <<end condition>>
    return Recursive(n - 1) + Recursive(n - 2);
}

<<DP Function>>
int DP(int n)
{
    <<0,1 condition>>
    for i,n
        new = old1 + old2
        <<swap new,old1,old2>>
    return old1;
}

Matrix Exponentiation

通过将递推公式转化为矩阵乘法的形式，由于格式很完美，可以推出 $n$ 次项通式, 具体证明可看参考。

这里需要注意的是，这个公式只适用于$0,1,1,2..$ 这个数列,如果以其他为起始的话，推出的公式并不是很通用
比如以$5,5,10..$ 这样的数列，展开的矩阵会不太通用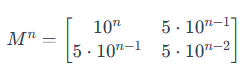

撇开其他数列，回到原来的数列，矩阵形式$a^n$十分适合做快速幂。时间复杂度为$O(log_2N)$

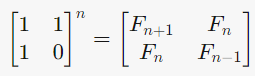
<<MatrixExponentiation Function>>
int MatrixExponentiation(int n)
{
    <<init>>
    matrix2 orig = {{1,1},{1,0}};
    matrix2 result = {{1,0},{0,1}};
    <<FastPow>>
        <<matrix pow>>
    <<FastPow>>
    return result;
}

矩阵幂推出的算法，我们可以借此推一个通项公式，虽然时间复杂度不变，但是可以获得一点常数级的优化（避免做矩阵乘法）

<<FastFib Function>>
int FastFib(int counter)
{
    <<end condition>>
    if even counter return Fn(2Fn+1 - Fn);
    else return (Fn+1)^2 + (Fn)^2;
}

Conclusion

当然，还可以借以上推出通用公式$f_n = xf_{n-1} + yf_{n-2}$，不过要符合以下形式

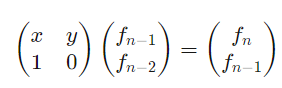
还有一些需要注意的点

当数字很大的时候，因为要进行大数运算，所以需要乘一个$O(n)$ 的复杂度，此时，快速矩阵幂的速度会比通项公式慢很多。在小规模（在100以内）的时候，用dp即可，因为矩阵乘法也会耗时。当大数时，可以使用Karatsuba multiplication，相对于普通乘法$O(n^2)$的时间复杂度，可以优化到$O(n^{log_23}) \approx O(n^{1.58})$ 的时间复杂度,简单来说就是做二分，然后每次二分做三次乘法运算。

int Karatsuba(int x, int y)
    // b 为 10, 10进制
    <<if x, y low, do naive>>
    <<get highbits & lowbits for x,y>>
    <<recursive for a,d,e>>
    return a*b^n + e*b^(n/2) + d;
}

Introduction:

F(n) = F(n - 1) + F(n - 2):

Matrix Exponentiation

Conclusion

Reference: